Figure 1: stepwise behavior in self-supervised learning. When training common SSL algorithms, we find that the loss descends in a stepwise fashion (top left) and the learned embeddings iteratively increase in dimensionality (bottom left). Direct visualization of embeddings (right; top three PCA directions shown) confirms that embeddings are initially collapsed to a point, which then expands to a 1D manifold, a 2D manifold, and beyond concurrently with steps in the loss.
It is widely believed that deep learning’s stunning success is due in part to its ability to discover and extract useful representations of complex data. Self-supervised learning (SSL) has emerged as a leading framework for learning these representations for images directly from unlabeled data, similar to how LLMs learn representations for language directly from web-scraped text. Yet despite SSL’s key role in state-of-the-art models such as CLIP and MidJourney, fundamental questions like “what are self-supervised image systems really learning?” and “how does that learning actually occur?” lack basic answers.
Our recent paper (to appear at ICML 2023) presents what we suggest is the first compelling mathematical picture of the training process of large-scale SSL methods. Our simplified theoretical model, which we solve exactly, learns aspects of the data in a series of discrete, well-separated steps. We then demonstrate that this behavior can be observed in the wild across many current state-of-the-art systems.
This discovery opens new avenues for improving SSL methods, and enables a whole range of new scientific questions that, when answered, will provide a powerful lens for understanding some of today’s most important deep learning systems.
Background
We focus here on joint-embedding SSL methods — a superset of contrastive methods — which learn representations that obey view-invariance criteria. The loss function of these models includes a term enforcing matching embeddings for semantically equivalent “views” of an image. Remarkably, this simple approach yields powerful representations on image tasks even when views are as simple as random crops and color perturbations.
Theory: stepwise learning in SSL with linearized models
We first describe an exactly solvable linear model of SSL in which both the training trajectories and final embeddings can be written in closed form. Notably, we find that representation learning separates into a series of discrete steps: the rank of the embeddings starts small and iteratively increases in a stepwise learning process.
The main theoretical contribution of our paper is to exactly solve the training dynamics of the Barlow Twins loss function under gradient flow for the special case of a linear model \(\mathbf{f}(\mathbf{x}) = \mathbf{W} \mathbf{x}\). To sketch our findings here, we find that, when initialization is small, the model learns representations composed precisely of the top-\(d\) eigendirections of the featurewise cross-correlation matrix \(\boldsymbol{\Gamma} \equiv \mathbb{E}_{\mathbf{x},\mathbf{x}’} [ \mathbf{x} \mathbf{x}’^T ]\). What’s more, we find that these eigendirections are learned one at a time in a sequence of discrete learning steps at times determined by their corresponding eigenvalues. Figure 2 illustrates this learning process, showing both the growth of a new direction in the represented function and the resulting drop in the loss at each learning step. As an extra bonus, we find a closed-form equation for the final embeddings learned by the model at convergence.
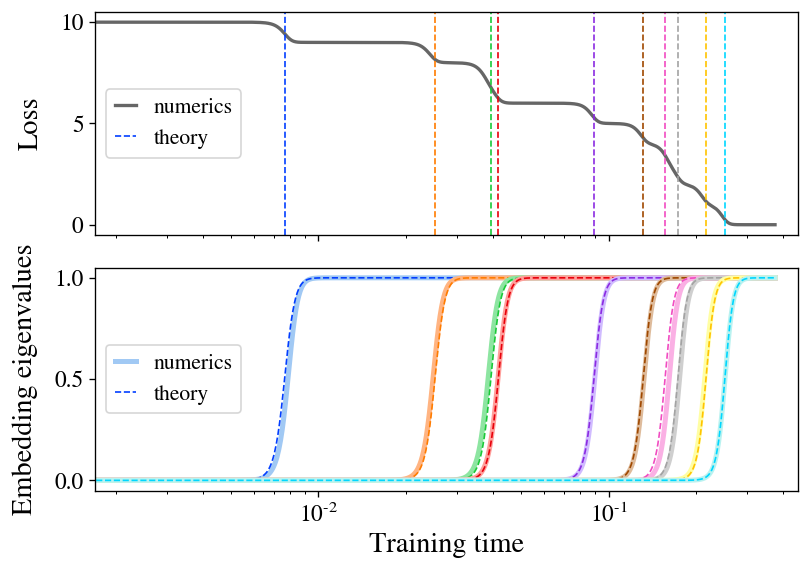
Figure 2: stepwise learning appears in a linear model of SSL. We train a linear model with the Barlow Twins loss on a small sample of CIFAR-10. The loss (top) descends in a staircase fashion, with step times well-predicted by our theory (dashed lines). The embedding eigenvalues (bottom) spring up one at a time, closely matching theory (dashed curves).
Our finding of stepwise learning is a manifestation of the broader concept of spectral bias, which is the observation that many learning systems with approximately linear dynamics preferentially learn eigendirections with higher eigenvalue. This has recently been well-studied in the case of standard supervised learning, where it’s been found that higher-eigenvalue eigenmodes are learned faster during training. Our work finds the analogous results for SSL.
The reason a linear model merits careful study is that, as shown via the “neural tangent kernel” (NTK) line of work, sufficiently wide neural networks also have linear parameterwise dynamics. This fact is sufficient to extend our solution for a linear model to wide neural nets (or in fact to arbitrary kernel machines), in which case the model preferentially learns the top \(d\) eigendirections of a particular operator related to the NTK. The study of the NTK has yielded many insights into the training and generalization of even nonlinear neural networks, which is a clue that perhaps some of the insights we’ve gleaned might transfer to realistic cases.
Experiment: stepwise learning in SSL with ResNets
As our main experiments, we train several leading SSL methods with full-scale ResNet-50 encoders and find that, remarkably, we clearly see this stepwise learning pattern even in realistic settings, suggesting that this behavior is central to the learning behavior of SSL.
To see stepwise learning with ResNets in realistic setups, all we have to do is run the algorithm and track the eigenvalues of the embedding covariance matrix over time. In practice, it helps highlight the stepwise behavior to also train from smaller-than-normal parameter-wise initialization and train with a small learning rate, so we’ll use these modifications in the experiments we talk about here and discuss the standard case in our paper.
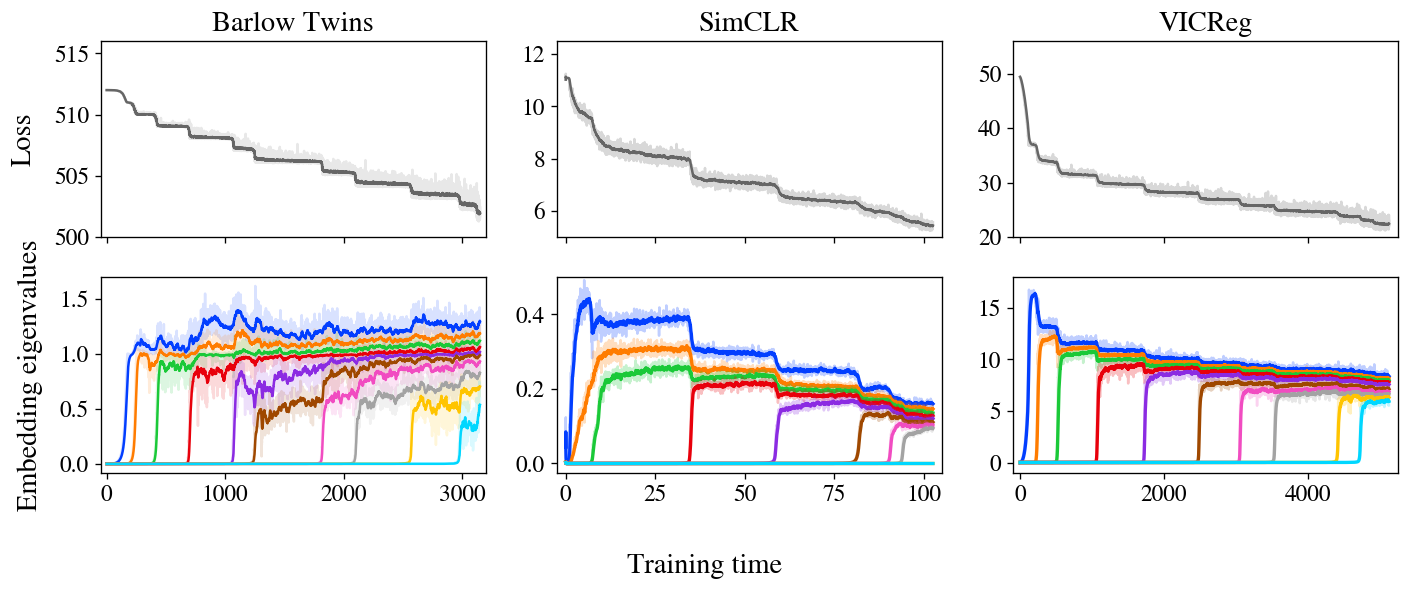
Figure 3: stepwise learning is apparent in Barlow Twins, SimCLR, and VICReg. The loss and embeddings of all three methods display stepwise learning, with embeddings iteratively increasing in rank as predicted by our model.
Figure 3 shows losses and embedding covariance eigenvalues for three SSL methods — Barlow Twins, SimCLR, and VICReg — trained on the STL-10 dataset with standard augmentations. Remarkably, all three show very clear stepwise learning, with loss decreasing in a staircase curve and one new eigenvalue springing up from zero at each subsequent step. We also show an animated zoom-in on the early steps of Barlow Twins in Figure 1.
It’s worth noting that, while these three methods are rather different at first glance, it’s been suspected in folklore for some time that they’re doing something similar under the hood. In particular, these and other joint-embedding SSL methods all achieve similar performance on benchmark tasks. The challenge, then, is to identify the shared behavior underlying these varied methods. Much prior theoretical work has focused on analytical similarities in their loss functions, but our experiments suggest a different unifying principle: SSL methods all learn embeddings one dimension at a time, iteratively adding new dimensions in order of salience.
In a last incipient but promising experiment, we compare the real embeddings learned by these methods with theoretical predictions computed from the NTK after training. We not only find good agreement between theory and experiment within each method, but we also compare across methods and find that different methods learn similar embeddings, adding extra support to the notion that these methods are ultimately doing similar things and can be unified.
Why it matters
Our work paints a basic theoretical picture of the process by which SSL methods assemble learned representations over the course of training. Now that we have a theory, what can we do with it? We see promise for this picture to both aid the practice of SSL from an engineering standpoint and to enable better understanding of SSL and potentially representation learning more broadly.
On the practical side, SSL models are famously slow to train compared to supervised training, and the reason for this difference isn’t known. Our picture of training suggests that SSL training takes a long time to converge because the later eigenmodes have long time constants and take a long time to grow significantly. If that picture’s right, speeding up training would be as simple as selectively focusing gradient on small embedding eigendirections in an attempt to pull them up to the level of the others, which can be done in principle with just a simple modification to the loss function or the optimizer. We discuss these possibilities in more detail in our paper.
On the scientific side, the framework of SSL as an iterative process permits one to ask many questions about the individual eigenmodes. Are the ones learned first more useful than the ones learned later? How do different augmentations change the learned modes, and does this depend on the specific SSL method used? Can we assign semantic content to any (subset of) eigenmodes? (For example, we’ve noticed that the first few modes learned sometimes represent highly interpretable functions like an image’s average hue and saturation.) If other forms of representation learning converge to similar representations — a fact which is easily testable — then answers to these questions may have implications extending to deep learning more broadly.
All considered, we’re optimistic about the prospects of future work in the area. Deep learning remains a grand theoretical mystery, but we believe our findings here give a useful foothold for future studies into the learning behavior of deep networks.
This post is based on the paper “On the Stepwise Nature of Self-Supervised Learning”, which is joint work with Maksis Knutins, Liu Ziyin, Daniel Geisz, and Joshua Albrecht. This work was conducted with Generally Intelligent where Jamie Simon is a Research Fellow. This blogpost is cross-posted here. We’d be delighted to field your questions or comments.